Журнал "Квадрат" #2: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Приветствие

Здравствуйте, уважаемые читатели. Надеюсь, прежде чем приступить к сборке фигур, вы подготовили должным образом своё рабочее место? А то придётся в самый ответственный момент броситься искать либо клей, либо ножницы, а это создаст ненужную сумятицу во время работы.

Если вы впервые посетили рубрику Полный разворот, то будет полезным ознакомиться с нашим первым выпуском.

Фигура #4. Пирамида

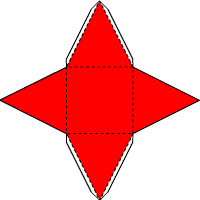
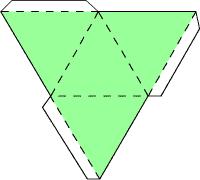
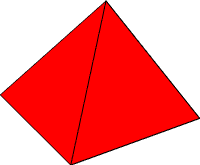
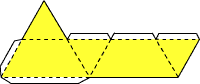
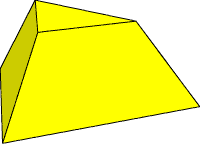
Наша четвёртая (в общем) фигура - это четырёхугольная пирамида. Кликнув по развёртке пирамиды, вы получите увеличенный рисунок. Распечатайте или перерисуйте развёртку на плотную бумагу.

Надеюсь, вы не успели позабыть, чем отличаются друг от друга сплошные и пунктирные линии? Но, на всякий случай, никогда не мешает заглянуть в первый выпуск рубрики, где всё подробно описано.

Склеив пирамиду, можно заметить, что она удивительно похожа на... тетраэдр (фигура #2). Тетраэдр - это правильная треугольная пирамида.

Однако развёртки этих фигур сильно отличаются. Дело в том, что у одной фигуры может быть порой несколько равноценных способов развёртки. В первом выпуске мы приводили одну развёртку тетраэдра, сейчас мы приведём другую, по которой сразу видно, что фигуры #2 и #4 очень похожи.

Можете попробовать снова склеить тетраэдр, но уже по новой развёртке. Щелчок по развёртке увеличит изображение.

Готовый тетраэдр, или треугольную пирамиду, вы можете увидеть в прошлом выпуске, здесь же приводим только изображение четырёхугольной пирамиды.

Фигура #5. Срезанный тетраэдр

Много интересных фигур можно получить, срезав часть простой фигуры. Фигура #5 получена именно таким способом: у тетраэдра - простейшего правильного многогранника - срезана одна вершина. Или, по другому, получилась усечённая треугольная пирамида.

На изображениях представлены развёртка этой фигуры и уже готовая фигура.

Фигура #6. Брус

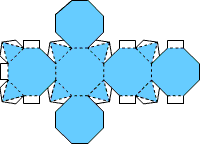
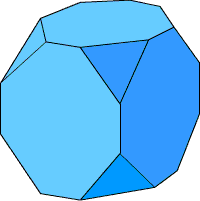
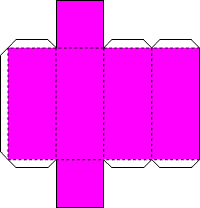
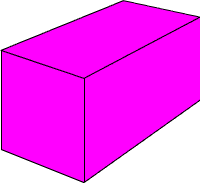
Также новые фигуры можно получать путём удлинения некоторых рёбер уже известных фигур. Например, следующая фигура сродни кубу (фигура #1), только более вытянутая в одну сторону - это брус.

Развёртки куба и бруса тоже очень похожи. Развёртка бруса и готовая фигура приведены на рисунках.

Фигура #7

И, напоследок, самая сложная в этом выпуске фигура. Склеивая её будьте особенно аккуратны. Она состоит из шести восьмиугольников и восьми треугольников. И если внимательно присмотреться, то можно заметить, что фигура #7 получается из обыкновенного куба, если срезать у него все его вершины.

На этом второй выпуск рубрики завершён. Пишите нам: e-Quadrat@narod.ru.

Автор и ведущий рубрики: Квадрат.

Предыдущий выпуск рубрики можно посмотреть здесь.

Следующий выпуск рубрики.

Дата последней редакции: Полный разворот © 1990-2016